First Steps

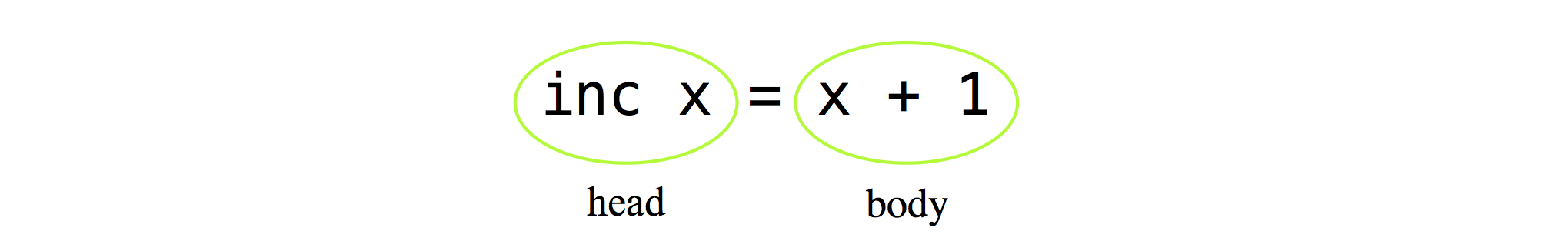
Values, functions, and types are the fundamental building blocks of a Haskell program; so, before we get started writing code, let's have a quick (and for now quite superficial) look at what these terms mean.

Values

Values are terms, such as 5 (an integer number), "Hello World!" (a character string), and 3.141 (a floating point number). Values are processed by functions. For example, addition + takes two numbers and produces a new number, namely the sum of the two input values; ++ takes two strings and produces a new string by concatenating the two input strings; length takes a string and produces a number, namely the length of the input string. In other words, functions, such as +, ++, and length, are mappings from input values to output values.

We can combine multiple values and functions, by using the result of a function application as input value for another function, as in

length ("Hello " ++ "World!")

The application of ++ to "Hello " and "World!" results in the string "Hello World!", which is the input value for the function length. Such a composition of values and functions is called an expression or term.

Types

Values can be grouped into sets with similar properties. For example, values which represent integers, strings, booleans, or floating point numbers. We call such sets of values types. Some examples of types which are present in most programming languages are the following:

We write 1 :: Int or "Hello" :: String to indicate that the values 1 and Hello have the the type Int and String, respectively. Hence, 1 :: Int can be read as “1 has type Int”.

Types essentially describe sets of values with similar properties and help us to distinguish correct from erroneous programs. For example, the expression 1 + "abc" contains a type error, because the string value "abc" does not match the type of argument expected by +. We call an expression without type errors well typed. Programming languages that enforce a rigorous type discipline are often called strongly typed languages. Type errors should generally be regarded as a hint by the programming system, telling us that part of our program do not make sense —the program is inconsistent— and they are one of the means by which the programming system helps us write better programs.

Functions

We have seen that, by applying functions to values, we can compute new values; but, how can we define new functions? Let us start with a simple example and write a function that increments a number by the value 1; let us call this function inc. So, the application inc 10 should produce 11, inc 11 should produce 12, and so forth — in other words, for any number x, the expression inc x, should yield x + 1. This general rule is formalised by the following function definition:

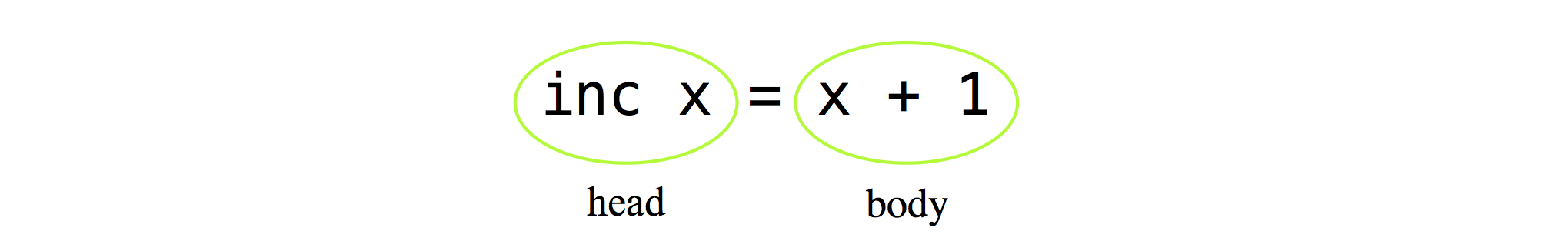
inc x = x + 1

A function definition comprises a head and a body separated by an equals sign. The head consists of the name of the function as well as names for the arguments to the function. In our example, there is only one argument denoted by the x. When inc is applied to an argument value, the result of the application is computed by replacing all occurrences of the variable x in the function body by the argument value:

inc 2  ⇒  2 + 1  ⇒  3

The arrow “ ⇒ ” represents a step in progressing from an expression to the value denoted by that expression. This process is called expression evaluation and corresponds to the execution of a program.

We can apply the function inc multiple times to a value by nesting the function application:

inc (inc 5)  ⇒  inc (5 + 1)  ⇒  inc 6  ⇒  6 + 1  ⇒  7

In our example, the choice of the name for the variable x and the function inc was arbitrary. There are, however, some syntactic restrictions for variable and function names in Haskell: the name of a function or variable

Moreover, when defining new functions, we have to be careful not to use a function name that does already carry a meaning, such as length. In programming languages, the names of objects, such as variables, are often called identifiers.

If we use an identifier the compiler does not know, as for example in the following incorrect definition of inc

inc x = y + 1

we will get an error message from the compiler of the form

Not in scope: `y'

which means that the variable y appears at a point in the programm where it is not defined.

Type Signatures

Functions map input values to output values, for example, inc maps integers to integers, or pictorially

PIC

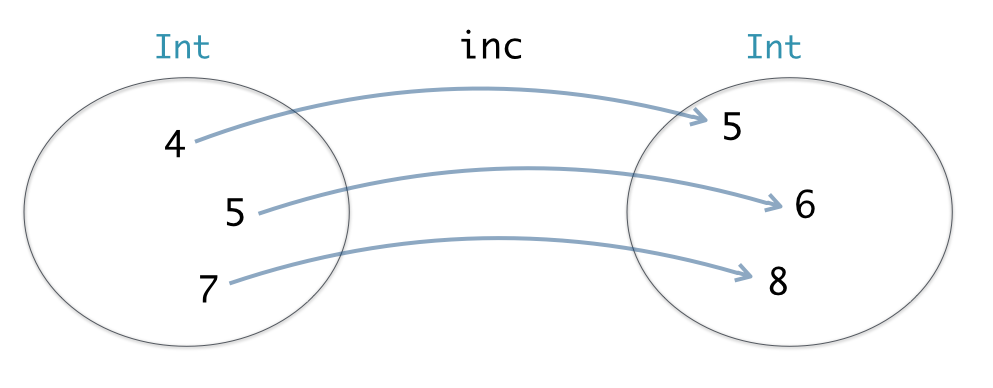
Thus, we denote the type of inc as Int -> Int. Overall, a complete function definition appears as follows:

inc :: Int -> Int     -- type signature
inc x = x + 1         -- function equation

Function signatures are optional, but they provide documentation for other programmers and help the Haskell system to spot type errors (i.e., inconsistencies between what we think a function is doing and what it is actually doing). In the above example, also note how Haskell allows us to annotate function definitions with comments in plain English by introducing these annotations with -- (a sequence of two minus signs). Such comments are disregarded by the computer, but may help other humans reading our program to understand its purpose. Comments introduced by -- extend until the end of the current line. Alternatively, we can enclose the text of a comment in {- and -}. That second form of comments may extend over multiple lines and may be nested.

In general, two functions, such as inc and double,

double :: Int -> Int
double x = 2 * x

may have the same type, but perform different operations. Nevertheless, like values of the same type, functions of the same type have something in common: they accept and produce values of the same kind.

As an example of a function with a type different from inc and double consider

exclaim :: String -> String
exclaim sentence  = sentence ++ "!"

The functions inc and double expect integers as arguments, whereas exclaim expects a string. Consequently, the expression inc "abc" is nonsensical and leads to a type error.

Multiple Arguments

We can compute the average value of the two floating point values 3.0 and 4.0 as follows:

(3.0 + 4.0) / 2.0

If we generalise this to computing the average of two numbers a and b, we get

(a + b) / 2.0

which we can turn into a function with two arguments as follows:

average :: Float -> Float -> Float
average a b  = (a + b) / 2.0

So, we have

average 3.0 4.0  ⇒  (3.0 + 4.0)/2.0  ⇒  3.5

The type of a function with more than one argument separates the arguments with an arrow (->). This symmetry in notation between argument types and the result type may be somewhat surprising at first, but there is a good reason for it.

You can view a function with two arguments, such as average, as a box with two free slots:

PIC

Once the function is applied to an argument of type Float, the first slot is filled, and it results in a new box with only a single free slot remaining, or in other words, it results in a new function which maps a value y provided as an argument to (3.0 + y)/2.0.

PIC

Only when the second argument is provided, and all slots are filled, can the function be fully evaluated and return the result value of type Float:

PIC

This means that, conceptually, we can view average as a function which, when applied to a single Float, will return a new function from Float to Float, or as a function which takes two Float values to produce a Float. In fact, Float -> Float -> Float is just short hand for Float -> (Float -> Float), as -> is right associative. Application is left associative, so

average 3.0 4.0

is just short hand for

(average 3.0) 4.0

Functions of multiple arguments that can be applied to their arguments one at a time (as is the case with average) are called curried functions (after the mathematician Haskell B. Curry — the Haskell language was named after him as well). In Haskell, all functions of multiple arguments are curried by default.

In our diagram, a value is a box without any empty slots, just like a function which has been applied to all its arguments. As we will see later, values and functions are treated almost the same in Haskell.

Writing Code

Now that we know about the basics, let's define and test the functions we discussed above. For our demos, we are using Haskell for Mac, an integrated programming environment based on the Glasgow Haskell Compiler for Mac OS X. However, as an alternative, you can simply use the Glasgow Haskell Compiler's command line interpreter in combination with any editor you like.

In Haskell for Mac, we edit the program in the module editor. Once a function is defined, we can use it in the playground, and the results, as well as the types of the results, will automatically be displayed. If there is an error in the program (wrong variable name in the screencast), an error marker appears and by clicking on it, we can see the exact error message.

The following screencast shows how to do essentially the same with an editor (using AquaEmacs here) and the Glasgow Haskell Compiler Interpreter (ghci) running in a shell. The main difference is that we have to save and reload the program file after each edit and that we have to relate error messages to program locations by way of the line numbers contained in each error message.

Infix and Prefix Application

Functions like + and * are binary functions, that is, functions which expect exactly two arguments, just like our average function. When we want to apply average, we first write the function name and then the arguments

average 6.9 7.25

while with addition and multiplication, we place the function in-between the arguments:

1   + 5
3.4 * 7.2

We call the former notation prefix, as the function appears before the arguments, and the latter infix, as it is in-between its argument. We can easily convert an infix function into a prefix one by simply placing it in parenthesis:

(+) 1   5
(*) 3.4 7.2

and conversely, we can use a regular binary function as infix operator by placing its name between backquotes:

6.9  `average` 7.25

Binary functions in backquotes are, by default, left associative, this means that multiple applications, as in

6.9  `average` 7.25 `average` 3.4

are implicitely grouped to the left; so, the above expression is the same as

(6.9  `average` 7.25) `average` 3.4

Which notation you use is a matter of style. In general, people can parse arithmetic expressions much more easily if they are in infix notation.

A First Glance at Overloading

All serious programming languages provide some functions whose argument types are not restricted to a single type, but instead a whole family of types is admitted. For example, both 1 + 2 (where the arguments are of type Int) as well as 1.5 + 1.2 (where the arguments are of type Float) make sense. Consequently, the function + simultaneously has the type

(+) :: Int -> Int -> Int

as well as the type

(+) :: Float -> Float -> Float

We call functions, such as +, overloaded functions; the name of an overloaded function carries more than just one meaning as witnessed by the multiplicity of type signatures. The motivation for permitting overloaded functions, such as +, is that it would be awkward to enforce the use of two different symbols —that is, two different function names— for the two cases of adding integers or adding floating-point numbers. (Note that Haskell requires us to use the prefix notation of an operator in a type signature; i.e., we write (+) and not just +.)

Unfortunately, all of this means that, given our current knowledge, we cannot denote the type of + in a single type signature of the form (+) :: type; instead, we have to resort to a family of type signatures (one for each possible type of +). To improve on this, we need to consider additional notation, where we exploit the fact that both argument types and the result type in one particular use of + are always identical. In other words, we might say that + has type a -> a -> a where a is either Int or Float. In fact, Haskell does not restrict a to only Int or Float, but instead allows any numeric type (most of which we have not encountered yet). We denote the set of numeric types by Num and generally call such sets of types type classes.

Using the type class Num, we can specify the type of + to be a -> a -> a, where the type a is a member of set Num, or, using mathematical notation a ∈ Num. Haskell abbreviates a ∈ Num to Num a and places it in front of the function type separated by a double arrow =>. Hence, the closed form of the type signature for + is

(+) :: Num a => a -> a -> a

Other binary arithmetic operations, such as - and *, have the same type. Note how types, such as Int and Float, as well as type classes, such as Num, have names starting with an upper case letter, whereas place holders, such as a, have names starting with a lower case letter. This convention simplifies reading type signatures and is enforced in Haskell. We call place holders in types, such as a above, type variables. They are important in programming languages that have a sophisticated type system.

In addition to Num, another important type class is Eq. It contains all those types for which the function == is defined, which checks whether its two arguments are equal. All types that we have encountered so far, except function types, are part of Eq. So, all of the following make sense:

2 == 2  ⇒  True

5.0 == 6.0  ⇒  False

(“Hello ” ++ “World!”) == “Hello World!”  ⇒  True

The type of == is

(==) :: Eq a => a -> a -> Bool

where Bool is the type of Boolean values False and True.

Another important type class is Show. It contains all types for which the system knows how to convert them to a string representation, and the most important function of this class of values is the show function:

show :: Show a => a -> String

All the basic types we have looked at are in this type class. For example:

show 123  ⇒  “123”

show 1.75  ⇒  "1.75”

show False  ⇒  “False”

show “False”  ⇒  "\"False\""

It is important to note that the Int value 123 and the string "123" are two fundamentally different objects, same for the boolean value False and the string "False". As we can see in the last example, if we apply show to a value which is already a string, it returns a different string, containing the opening and closing quotes as additional characters.

Functions are not in the type class Show, so if we try and apply show to the function inc, for example, the compiler will complain:

    No instance for (Show (Int -> Int)) arising from a use of `show'
    Possible fix: add an instance declaration for (Show (Int -> Int))
    In the expression: show inc
    In an equation for `it': it = show inc

The compiler message No instance for (Show (Int -> Int)) means that the type Int -> Int is (so far) not in in the type class Show. We will later see that we can extend type classes, and the compiler suggests to do so as a fix.

The function show is also invoked whenever we enter an expression in a Haskell for Mac playground or at the GHCi prompt: after the expression is evaluated, the system tries to convert it to a string using the show function, so it can print it. Therefore, if we just enter a function in a playground or at the GHCi prompt, we will see a similar error message. All this is illustrated in the following screencast.

Frequently used type classes and overloaded functions. We will cover type classes and overloading in more detail in later chapters. For now, here is an overview of some frequently used type classes, and some overloaded operations on these type classes.

We will introduce more type classes and operations as we use them. If you want to find out more about a type class, select its name and type ⌘-i in Haskell for Mac, or use :info TYPECLASS-NAME in GHCi.

Exercises

  1. What is the difference between the type Char and the type String? Do the two expressions "a" and 'a' represent the same value?

  2. Given the function definition

    square :: Int -> Int
square x = x * x

    and the previous definitions of inc and double. What is the value of

    1. inc (square 5)

    2. square (inc 5)

    3. average (inc 3) (inc 5)

  3. If you remove the optional type annotation from the above definition of square, what type will the compiler infer? You can find out by pressing ⌘-i in Haskell for Mac, while your cursor is on the function name, or by typing :type square or :t square in GHCi.

  4. Which of the following identifiers can be function or variable names?

    If you are unsure, replace the function name in your square definition from Exercise 2 with each of these identifiers to see whether the compiler complains and what the error message looks like.

  5. Define a new function showResult, that, for example, given the number 123, produces a string as follows:

    showResult 123  ⇒  "The result is 123"

    Use the function show in the definition of the new function.

  6. Write a function showAreaOfCircle which, given the radius of a circle, calculates the area of the circle,

    showAreaOfCircle 12.3  ⇒  "The area of a circle with radius 12.3cm is about 475.2915525615999 cm^2"

    Use the show function, as well as the predefined value pi :: Floating a => a to write showAreaOfCircle.